物体の運動を数学的に記述する手法は運動の第2法則とよばれ、運動の第2法則は、慣性系で計測した質量m(t)と速度v(t)の積で定義された運動量をp(t)、力をF(t)として(運動量については4-4節で説明)、
物体のある瞬間における運動量の時間変化率は、加えられた力に一致する。
⇓
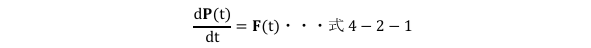
という形式の微分方程式で表され、この方程式を状況に適した条件を設定することにより物体の運動を解析します。
また、運動の第2法則は力の定義式でもあって、質量と速度が定義可能であることから運動量を定義することができるため、力は運動量の時間変化率が決定すると読んで力という物理量が存在すると宣言できます。そして、一旦、力を定義することが可能と解釈すると、実際は逆に読んで力という物理量が物体に作用すると結果として物体の運動量の時間変化が生じると解釈して運動の解析に使用します。
さらに、この方程式はロケットの運動のように燃料を噴射し続けて質量が変化する場合や、小惑星が合体し質量を変化させながら宇宙空間を運動する場合にも使える形ですが、通常はこれらの影響は考慮しないで質量は変化しないものとして、慣性系で計測した位置ベクトルをr(t)と表示した、
【運動の第2’法則】
質量を持った物体は、力を加えられると加速度を生じ、質量と加速度の積は加えられた力に一致する。
⇓
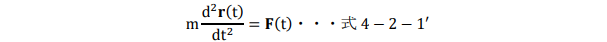
の形式のものが教科書に採用されているので、本稿ではこの形式の方程式を運動の第2法則とします。
この物体の座標の微分で表示した形式の運動方程式も運動量を用いた形式のものと同様に力の定義式とも考えることができ、その際、適当に単位を設定すれば良いわけですが、いい加減に設定すると調整に必要な定数を導入しなければならなくなるため、長さをメートル[m]、時間を秒[s]で計測して、質量には[kg]を単位として用いるとき、1[kg]の質点に1[m/s2]の加速度を生じさせる力を1ニュートン[N]と定義することにより余計な調整を不要なものとすることができます。
こうして、運動の第2法則として式4-2-1’を採用することにして、この微分方程式を運動方程式とよび、質量m[kg]の物体に力F[N]が作用した結果d2r(t)/dt2の加速度が生じると解釈することで、解析的、数値的に解くことで物体の運動を解析していくことになります。
ちなみに、空間間隔、時間、質量の決め方については、人間の活動から人間の活動に適当な定義で、基準になるそれぞれの量を決定する道具を作り出して測定してきたようです。
例えば、質量なら元々は水1[l]の質量を1[kg]とするとして、同じ重さの金属の重りを作成してこれを基準にして重さを測定するということをしてきたようで、基準となる道具を複製することで基準を引き継いでいたし、長さや時間に関しても地球の大きさや自転の時間を基準にして定義してきたようですので、人間の都合で決めた量と言え、あまり気にしなくてもよいでしょう。ただし、最近、これらの定義が変わり、厳密に決定されるようになったようですので興味のある方は大学入学後にでも各自調査してみてください。