冒頭で述べたように、力学は力の作用と加速度を関連付ける何らかの関係から最終的に物体の座標を決定することが目標であるため、物体の位置に関する物理量について説明します。
物体が力の作用を受けて空間内を運動するとき、使用している座標系で物体の座標値の組を時刻t[s]の関数としとして(x(t) , y(t) , z(t))と表すと、この座標値の組は原点から空間内における物体の位置へ向けた矢印で表されるため、向きと大きさを持つベクトル量であって特に位置ベクトルと呼ばれます。
そして、位置ベクトルをr(t)とすると
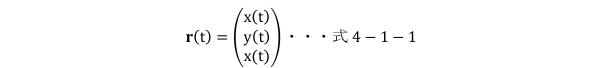
と表示できます。
また、時刻t1、t2の位置ベクトルの終点同士を接続した量も向きと大きさを持ち、こちらは変位ベクトルとよばれ、Δr(t)とすれば、
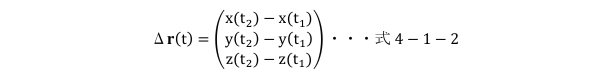
と表示できます(図4-1-6)。
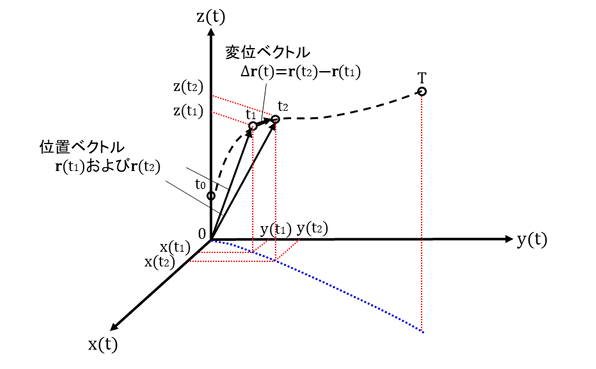
図4-1-6. 位置ベクトルと変位ベクトル