物体が空間内を運動するとき、軌道が時刻の関数として表示できれば運動は確定したといえるかということを問題にして、今、何らかの方法で時刻の連続な関数として現実の軌道が与えられていて獲得した関数のみを用いて軌道を描くことを考えることにします。
このとき、得られた軌道を表す関数のみを用いて描図しようとすると数の連続性により任意の時刻、および、この時刻に正に隣接する時刻を指定することはできないことから、各時刻の物体の位置を表す点と点を接続することで軌道を描くことになります。しかし、このことはグラフ上に適当な時間間隔で各時刻における物体の座標値の組を示す点を表示した上で、時間間隔が十分短ければ軌跡が滑らかな曲線軌道として観測できることを仮定して、可能性としては無数に存在する経路の中から隣接した点を直線で接続する経路を選択して軌跡の完成を目指すことを意味するため、軌道を描くためには各時刻間の座標値の組同士の間の間隙を接続する情報も必要になるということが分かります(図4-1-1)。
よって、以上のことから上記の方法で物体の軌道を一応は描くことができることは分かりましたが、物体の軌道を非常に短い直線を連ねて近似してよい根拠は、与えられた軌道を表す関数には存在しないため物体の軌道を決定するためには別の物理量を追加する必要があると結論できます。
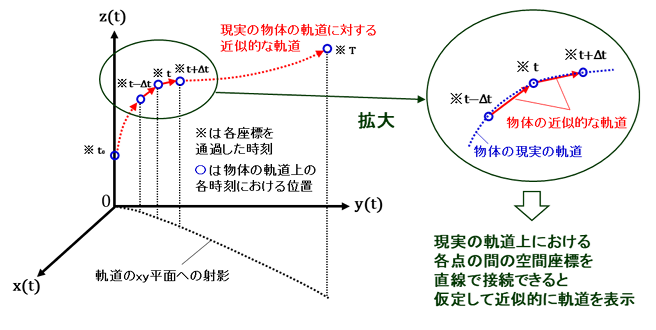
図4-1-1. 物体の空間座標のみから軌道を描図する方法
では、この事情を空間座標以外の時刻の関数も考慮することを含めて軌道を表示するという側面から考えることにして、再び、物体の軌道の座標値の組が力を介して直接求まる可能性を考慮すると、この手法では各瞬間の軌道が直線であることを仮定しなければならないことに加え、冒頭の記述から何らかの物理量が運動を決定することに合理性が無いことも加わり、当然、その可能性はありそうもありません。
また、次の候補として力と各時刻の座標値の組から得られる速度の関係が確定できれば、速度が各々の座標値の成分の時間変化率であることから、各時刻の位置と移動手段に関する情報が速度の関数形に含まれているため軌道が決定できますが、これも冒頭の記述より力と速度の関係を介して運動が決定する可能性はないと言えます。
従って、さらに速度の時間変化率である加速度の関数形が力から決定する手法を考えることになりますが、冒頭の加速度と力の考察より、力と加速度の関係を見出すことは可能と考えられるので、物体の運動の軌道を決定するためには、加速度と力を規定する数学的手段を見出して、各々の問題で必然的に加速度が規定される関係式を探求して、未知の関数である各々の時刻における座標値の組を割り出す手法を模索することが必要と言えます。
そして、関数を用いて物体の軌道を決定する手法が得られれば、基準となる時刻における座標と速度が分かっているとき、軌道上の各時刻における力と加速度の関係から加速度を決定することに始まり、加速度が速度の時間変化率であることから、加速度に時間間隔を乗じて各時刻の速度変化を算出して直前の時刻の速度を加算することで、わずかに時間が経過した時刻の速度を確定した上で、さらに、速度が各時刻の座標値の組についての時間変化率であることも考慮して、速度に時間間隔を乗じて各時刻の物体の位置の変化を算出して直前の時刻の座標値の組を加算することにより、僅かに時間が経過した時刻の物体の位置を決定するという作業を必要な時間内で実施すれば物体の軌道を決定することが可能になると結論できます(図4-1-2)。
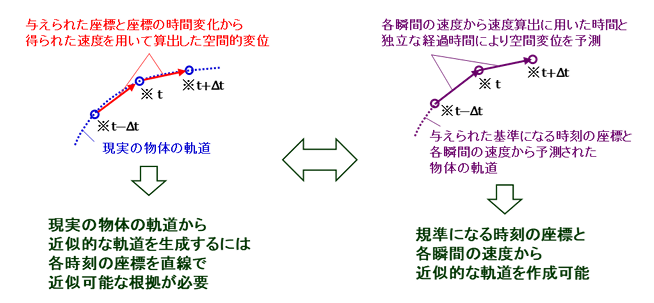
図4-1-2. 関数を用いた物体の軌道の描図
ちなみに、物体の軌道の関数のみから軌道を決定していく手法と加速度の関数から物体の軌道を決定する手法は一般に異なる結果が得られます。 しかし、離散的な関数から移動量を算出する方法と連続関数から移動量を予測する方法、双方において各区画で速度が一定とみなせる程度に時間間隔を十分短くすると、既知の離散的な軌道を非常に短い直線で近似したものを接続することと、軌道を予測する方法において加速度は速度の時間変化率であるという定義から連続な関数である加速度を用いて極めて連続的な離散的関数である速度を算出した後、同様に極めて連続的な離散的関数である速度から同様の性質を有する物体の座標を予測することは、どちらも極めて良い近似になると考えられるためにほぼ一致すると考えることができます(図4-1-3)。
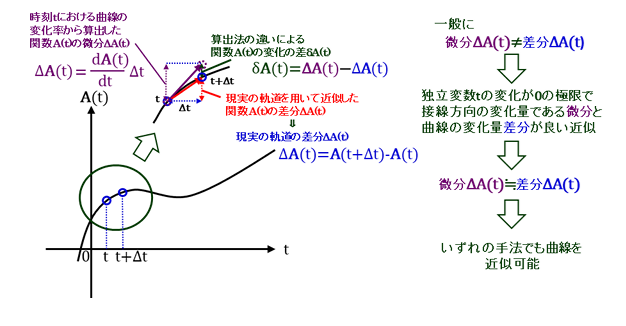
図4-1-3. 物体の軌道に対する近似方法の違いの影響
よって、関数を用いた手法のように、一旦、物体に作用する力から加速度を確定させる手段を獲得して、速度、座標値の組を自動的に確定させられる方法が得られることは、物体の運動を解析する手法として非常に魅力があり、この手法による運動の解析がニュートンによる力学の中心的な課題になります。ただ、本節の目的は力学の手法についての問題提起と力学で使用される物理量の紹介であるため、運動を解析するための一般論については次節で扱います。
さらに、図4-1-1と図4-1-2では空間内での物体の軌道に時刻を表示する形式によって、図4-1-3では一般的な物体の運動に関する物理量(A(t))を時刻の関数によって記述しましたが(今、運動の軌道を問題にしているためA(t)を座標値の組に置き換えて考えると)、同じ対象を空間内の軌道(座標値の組)で表したり、時刻の関数として軌道を表したりすることに疑問を持った人もいるかもしれないことと、同様のことが高校物理の教科書でも運動の成分を用いた形式で記載されていることから説明を加えることにします。
ただし、本来、物体の軌道は時刻と三つの空間座標を独立変数としてまとめた四次元の時空内において表されるべきですが、力学が軌道を時刻の関数として表示していることにより時間と空間が対等でないという問題を内包していることは一旦無視するとして、人類は四次元以上の次元を直接認識できないことから空間を1次元と2次元に減じて図4-1-1、図4-1-2のように物体の軌道上に時刻を表示する表現が、図4-1-3のように時刻の関数として得られた物体の軌道を各時刻において空間方向に射影することで生成された表現であることを説明します。
そのために、空間一次元(直線運動)の軌道と空間二次元(平面運動)の軌道を模式的に表示した図4-1-4を用いて解釈していくことにしますが、注意点として図4-1-3は横軸が時間軸に、図4-1-4は縦軸が時間軸になっています。これは力学では空間座標の組各々を時刻の関数で表す一方で、時空内の軌道という視点に準じて物体の運動を観測する場合には人類が地球の表面に存在していて水平方向に移動して生活しているためか、空間を水平方向に表示した方が軌道を認識しやすいことから生じた差異で、通常、時空内の軌道を考える場合は縦軸に時刻を横軸に空間成分を配置した図4-1-4の形式の図が用いられることが理由になります。
以上を念頭に、時空内における物体の軌道に準じた見方で時刻の関数で表された物体の軌道を空間内における物体の座標値の組で表示する方法を提示すれば、1次元の運動の例では、図4-1-4左図に示すように、各時刻における物体の位置を記録していって、基準になる時刻(通常時刻0における直線)の空間成分上に時空内の曲線から空間座標を射影して各点を通過した時刻を表示した図が、2次元の運動の例では、図4-1-4右図に示すように、時刻と直交する各時刻の平面上を通過する物体の位置を記録していって、基準になる時刻(通常時刻0における平面)の空間成分上に時空内の曲線から空間座標を射影して各点を通過した時刻を表示した図が空間内における物体の軌道を表示した図4-1-1、図4-1-2に対応します。また、図4-1-3の形式で時刻を独立変数として見たい場合は図4-1-4の形式の座標系を回転して横軸を時間軸にすれば必要な図が得られます。
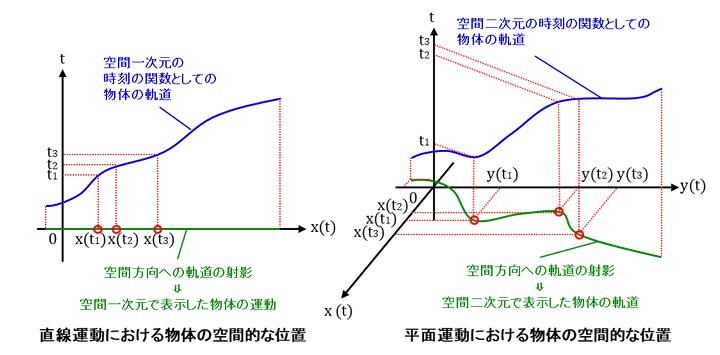
図4-1-4. 時空内の物体の軌道と空間方向への射影
加えて、時空という用語を用いたので相対性理論で登場する、時空内での物体の軌道や異なる座標系間の座標値の関係を可視化する時空図について少しだけ言及することにします。
時刻と空間座標、つまり、時空内の座標を独立変数にする見方は相対性理論以前にも波動現象や電磁気的現象などでとられていましたが、相対性理論は互いに運動する座標系間の時空の関係、つまり、独立変数間の関係そのものを対象とする意味で時空の性質を扱う物理の一分野と言え、基本的に物理学が時空内の座標を独立変数とすることから全ての物理学の基礎となる位置づけになります。
そのため、相対論的な時空の見方を元にして時空内の座標を独立変数に持つ物理量を解釈するという思考は自然な流れであり、人間活動に焦点を当てた速度帯では加速度運動の相対論的効果は問題にならず、加速度運動する座標系に対する他の座標系の座標値を扱う一般相対性理論はもちろん不要であるため、互いに等速度で運動する座標系間の座標値の関係を規定する特殊相対性理論における時空図に関連させて力学で用いる座標系について検討をすることにします。
特殊相対性理論における時空図は図4-1-5のように縦軸に時間軸、時間軸と直交するように空間軸を配して表示され、最も一般的な時空の変換では時間と空間が混在する変換になることが要請されるため、これらの単位を揃える必要性と人間活動を基準にした空間的間隔を[m]、時間的間隔を[s]とする単位系での時空の間隔の表示では相対論的効果の表れる光速の10%程度からの速度帯を扱うことが困難になる問題から(通常の単位で速度1000m/sと10000m/sの粒子の軌道を描図するだけで区別が困難)、時間は各時刻に光速c=3.0×108m/sを乗じて時間軸を引き伸ばして時刻を距離の単位[m]で表示することで、高速度域に特化した光速度を無次元の1とする単位系を用いて表現されます。
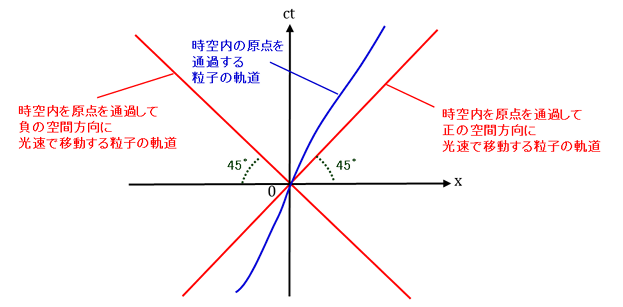
図4-1-5. 空間1次元を運動する粒子の時空図
一方、人間活動を基準にした速度域で時空内の座標値の関数として物理量を表示したければ、時間を秒、空間間隔をメートルで表示する通常の単位系において、1sで1m進む速さを1m/sと定義することで時間と空間間隔が等しいとみなすことができますが、この見方は、光速度で時間軸を引き伸ばす代わりに時間に速度1m/sを乗じて1mが時間の1sに対応すると解釈して時間も距離の単位で計測した人間活動に特化した速度域の時空図と結果的に等価になると考えられます。
このため、時空内における波動現象や電磁場(高校では時間変動する電磁場は基本的に扱いませんが)を表示するための座標系は図4-1-4の形式で表されることから、これらの分野における時空内の独立変数の組を表す同図は結果的に時空図に等価な表現となるもものの、時間と空間の単位が異なるため時空図に準じた表現と言えます。
また、変形しない物体の力学は物体の座標を時刻の関数として表示するため時空内における変形しない物体の軌道を決定しますが、時空内の座標を独立変数として扱う波動現象や電磁場と異なるのは物体の空間座標を時刻の関数として表示するという点であって、図4-1-4の座標系を回転させて横軸の時間軸を独立変数にして縦軸の空間軸を表した図4-1-3は、こちらも速度の定義が空間間隔と時間間隔を等しくするため結果的に時空図と等価になるものの完全に同じものでもないため、同図も図4-1-4とは異なる時空図に準じた表現と言えます。