物理学では、物理現象を記述する物理量を、座標や状態を表す物理量を独立変数とする関数として定義し、微小な独立変数の変化に対する関数の変化率を組み合わせて自然現象を決定する方程式を立式して、現象の境界において成立する条件を設定することで、状況に適合する関数を求めるという手法で物理現象を解析します。
これは数学の言葉を用いると、与えられた条件下で微分方程式を解くと表現され、独立変数が一つの微分方程式であれば「常微分方程式を解く」と、また、独立変数が複数であれば「偏微分方程式を解く」と表現されます。この微分方程式は高校数学では扱いが大きくありませんが、微分積分の概念を知っていれば理解可能の上、利用すると現象の理解が進むと考えられるため本編では扱うこととします。
そして、物理現象を表現する微分方程式を立式して、物理現象を記述する関数を決定すると、この関数を用いて現象の予測、確認、利用が可能になります。
ただ、この説明だけでは想像しにくいと思うので、比較的考え易い具体例である時刻を独立変数として物体の1次元の運動を解析する力学の問題を題材にして、高校物理で頻繁に現れる微分方程式に対して、状況の分析から立式を経て解を得るまでの手順を紹介することにします。
まず、物体の速度が変化する状況で何が起こるか考えると、物体に運動を変化させる作用が働いた結果、時々刻々と運動が変化することを、時刻をt、位置ベクトルの運動方向の成分を時刻の関数の意味でx(t)、時間変化しない物体の質量をm、物体に与えた作用を力f(t)とすることで、常微分方程式により表現したのが式2-1-1になります。
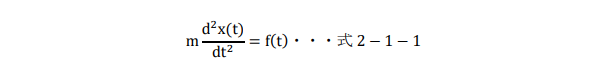
また、この方程式の意味は後の力学の章で説明しますが、簡単に述べると質量mの物体に力f(t)が作用した結果、速度の変化率である加速度d2x(t)/dt2が生じると解釈されます。
そして、一旦、運動を記述する微分方程式が得られたなら、微分方程式の型によって単純に積分したり、微分方程式特有の解法を用いたりして、微分方程式を満たす未知関数である位置ベクトルの運動方向の成分x(t)を求めて、物体の力学的挙動を解析します。